领悟10种数学思维，从此不怕数学！

心理学家马克思韦尔·马尔茨说：“所有人都是为成功而降临到这个世界上，但是有的人成功了，有的人没有，那是因为每个人使用大脑的方法不同。”

虽然每个人都有思维，但是思维的质量有差别，思维的质量直接影响人们做事的质量和生活的质量，决定了一个人是富有还是贫穷，是健康还是多病，是强大还是弱小，是幸福还是不幸。高质量的思维可以保证生活各个领域都朝着我们期望的方向发展，不良的思维习惯则会让我们付出巨大的代价，包括经济上和精神上的代价。

我国著名思想家楚渔，在其《中国人的思维批判》一书指出，导致中国落后的根本原因是传统的思维模式。他说，一百多年前我们苍白地复制西方人当时的创造，一百多年后我们仍然在苍白地复制西方人现在的创造。因为我们的思维方式落后了，使得我们既不能理解西方文化的精髓，也不能很好地传承和发展我们中华文化中的优良传统。

比如，中国有一则寓言叫《愚公移山》，西方也有一则寓言叫《明罗移山》。他们的处境一样，都住在大山里，被两座大山挡住了去路。中国老愚公的办法是动员全家，拿起锄头，挖山不止，而且准备一代代挖下去；老外明罗，他们是选择向专家求教。专家建议：搬出山去，另找一个适合自己居住的地方。这样既保护了环境又节省了劳动力，两全其美。

一样的境遇，不一样的选择，结果可想而知。也就是说，拥有先进的思维方式才能在面对繁杂的事务和困难的问题时应对自如，才能更好地学习、工作和生活。

数学学习中同样有许许多多先进的思维方式，培养和拥有这些思维方式，有利于快速准确地解决数学问题，提升学习兴趣和自信心，以及抓问题本质的能力。同时，也可以帮助我们应对那些数学思维水平要求极高的数学杯赛。

以下是我结合数学学科的特点，从众多的思维中归纳总结和提炼出来的10种数学思维，希望对家长在指导孩子学习时有所助益：

第一种 转化思维

第二种 逻辑思维

第三种 逆向思维

第四种 对应思维

第五种 假设思维

第六种 类比思维

第七种 创新思维

第八种 系统思维

第九种 形象思维

第十种 灵感思维

●转化思维的现状

在小学数学教材中，以章和节形式出现的数学知识是明线，连接所有章和节的数学思想方法是暗线。

数数知识是学生学习的主要目标，也是评价学习好坏的重要依据。数学思想方法是学生学习的调味品，由于不系统，老师水平参差不齐，学生学完后的感觉如同只见树木，不见森林，没有全局观。

小学阶段的数学知识点涵盖了计算、图形和实际应用三大类问题。这三种问题中应用题最棘手。其中一步应用题是属于最直白类型的，直接列算式写得数，而多步应用题往往不是直接通向问题的，它需要我们从给出的条件中得到新的信息，再逐步转化得到问题的最终答案。很多学生失败也就在这里，看到陌生问题就放弃或直接求助于家长。实际上，转化思维出了问题。

【例】：用简便方法计算 19×27＋190×5＋19×23

分析：这题可看成是由3个小算式构成的大算式，且每个小算式中都是两个数相乘的形式，这种特点比较适用于乘法分配律的逆用。要想逆用乘法分配律，3个算式中得有相同的数，而这个题中没有，所以先要转化。

解：原式＝19×27＋19×10×5＋19×23

＝19×27＋19×50＋19×23

＝19×（27＋50＋23）

＝19×100

＝1900

●转化思维的定义

转化思维，是指在解决问题的过程中遇到障碍时，通过改变问题的方向，从不同的角度，在分析理解题意的基础上把问题转化成与它相近或对等的问题，寻求最佳方法，使问题变得更简单、更清晰。

【例】有黑白两种棋子共300枚，按每堆3枚分成100堆，其中只有1枚白子的共27堆；有2枚或3枚黑子的共42堆；有3枚白子与有3枚黑子的堆数相等。那么在全部棋子中，白子共有多少枚？

分析：

（1）只有一枚白子的堆数＝有2枚黑子的堆数＝27

（2）有2枚或3枚黑子一共的堆数＝只有一枚白子与有0枚白子一共的堆数＝42，有0枚白子的堆数＝有3枚黑子的堆数＝42－27＝15

（3）有3枚白子的堆数＝有3枚黑子的堆数＝15

解：有0枚白子的堆数＋有1枚白子的堆数＋有2枚白子的堆数＋有3枚白子的堆数＝100

有2枚白子的堆数＝100－15－27－15＝43（堆）

白子的枚数＝15×0＋27×1＋43×2＋15×3＝158（枚）

●转化思维的几个方面

1、要素与要素的转化

①数与数的转化：这种转化方法在计算类型的题目中比较常见。如在进行加减法巧算时，会用到一种看成整数的方法，这种方法只改变了原数的形式，在结果上面却是对等的。在高年级，分数、小数的四则混合运算及巧算中，通常会出现分数与小数互化的情况。

【例】9999×2222＋3334×3333

题意理解：

（1）算式中没有相同的数，无法直接使用乘法分配律

（2）算式中9999与3333是3倍的关系

巧妙求解： 原式＝3333×3×2222＋3334×3333

＝3333×6666＋3334×3333

＝3333×（6666＋3334）

＝3333×10000

＝33330000

②形与形的转化：这种转化方法在解决图形问题时比较常见。一般形与形的转化会涉及到的方法有：三角形等底等高的性质，四边形中的等积变形、蝴蝶定理、燕尾定理的方法，圆形中的重叠法、旋转法、割补法等。通过这些方法，能够很直观地把原来的图形转化成容易求的图形。

【例】如下图，ABCD是边长为8厘米的正方形，梯形AEBD的对角线相交于O，三角形AOE的面积比三角形BOD的面积小16平方厘米，梯形AEBD的面积是多少平方厘米？

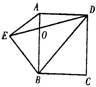
题意理解：

（1）S正方形ABCD＝8×8＝64 cm² AE∥BD

（2）S△BOD－S△AOE=16cm²

S△BOD＋S△AOD－（S△AOE＋S△AOD）＝16 cm²

（3）S梯形AEBD＝S△AEB ＋S△ABD

（4）通过分析，问题转化成求△AED与△ABD的面积和。

巧妙求解：

S△BOD－S△AOE=16cm²

S△ABD－S△AED=16cm²

S△ABD=8×8÷2=32cm²

S△AED=16cm²=S△AEB

S梯形AEBD=16+32=48cm²

③数与形的转化：这种转化方法在解决行程问题时比较常见。通过图形展示复杂的条件，通过数据进行周密的推理，最终达到解决问题的目的。

【例】甲、乙两车同时从A、B两地相向而行，在距A地80千米处相遇，相遇后两车继续前进，甲车到达B地、乙车到达A地后均立即按原路返回，第二次在距B地60千米处相遇。求A、B两地间的路程。

换个角度想一想：画图把甲乙两车的运动过程形象化，求出甲车走的路程。

巧妙求解：

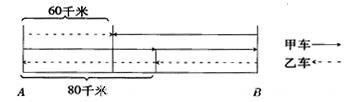
8×3＝240（千米）

240－60＝180（千米）

答：A、B两地间的路程是180千米。

2、知识与知识的转化

①横向转化：即知识点之间的迁移，这种转化方法在解决角度问题、按比例分配问题中较为常见。

【例】在下图中，∠A, ∠B, ∠C, ∠D,∠E,∠F和∠G的度数和是多少？

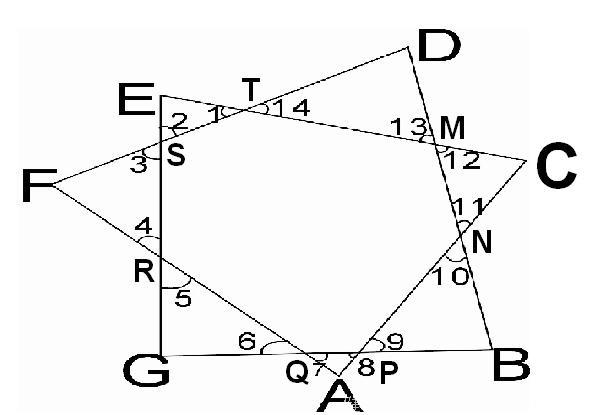
题意理解：

（1）∠1＋∠2＋∠E＝∠3＋∠4＋∠F＝∠5＋∠6＋∠G＝∠7＋∠8＋∠A＝∠9＋∠10＋∠B＝∠11＋∠12＋∠C＝∠13＋∠14＋∠D＝180

（2）七边形QRSTMNP的内角和为：180°×（7－2）＝900°

（3）∠1＝∠14 ∠2＝∠3 ∠4＝∠5 ∠6＝∠7 ∠8＝∠9 ∠10＝∠11 ∠12＝∠13

（4）∠A＋∠B＋ ∠C＋∠D＋∠E＋∠F＋∠G＝180°×7－（∠1＋……＋∠14）＝180°×7－2×（∠1＋∠2＋∠4＋∠6＋∠8＋∠10＋∠12）

（5）通过分析，问题就转化成求∠1＋∠2＋∠4＋∠6＋∠8＋∠10＋∠12的角度和。

巧妙求解：

七边形QRSTMNP的内角和＝180°－∠1＋180°－∠2＋180°－∠4＋180°－∠6＋180°－∠8＋180°－∠10＋180°－∠12＝180°×7－（∠1＋∠2＋∠4＋∠6＋∠8＋∠10＋∠12）＝900° 即∠1＋∠2＋∠4＋∠6＋∠8＋∠10＋∠12＝180°×7－900°＝360°

所以∠A＋∠B＋ ∠C＋∠D＋∠E＋∠F＋∠G＝180°×7－2×（∠1＋∠2＋∠4＋∠6＋∠8＋∠10＋∠12）＝180°×7－2×360°＝540°

②纵向转化：即对已知的条件进行深度分析，找出隐藏的信息。这种转化方法在解决和差倍问题、盈亏问题、数论问题、物体的体积、抽屉问题、分数应用题方面比较常见。

【例】某校有20个班，平均每个班46人，老师让每个同学用1991这4个数字中的1个或几个任意写出一个自然数。那么，至少有多少人写的数相同？

题意理解：

（1）学校一共有20×46＝920人。

（2）所有写出的自然数可以分成一位数、两位数、三位数和四位数

（3）通过分析，可以把列举出的自然数的个数看做抽屉，再根据抽屉原理进行解答。

巧妙求解：用1991中的一个或几个任意写出的自然数可以分类为：

①一位数：1、9 2个

②二位数：11、99、19、91 4个

③三位数：111、999、119、991、191、919 6个

④四位数：1991、1919、1199、9911、9191、9119 6个

不同的写法一共：2＋4＋6＋6＝18（个）

把18种不同的写法看成18个抽屉，又920＝18×51＋2

所以，至少有52人写的数相同。

3、知识与实际的转化

①生活问题数学化：即在生活问题的基础上建立一个数学模型，再用数学对应的方法去解决。

【例】某蔬菜公司收购到某种蔬菜104吨，准备加工后上市销售。该公司加工该种蔬菜的能力是：每天可以精加工4吨或粗加工8吨。现计划用16天正好完成加工任务，则该公司应安排几天精加工，几天粗加工？

题意理解：

（1）精加工天数＋粗加工天数＝16

（2）精加工吨数＋粗加工吨数＝104

巧妙求解：设该公司安排X天粗加工，安排Y天精加工。则：

X＋Y＝16

8X＋4Y＝104

解得：X＝10，Y＝6

答：该公司安排10天粗加工，安排6天精加工。

②数学问题生活化：即在生活中找到数学知识的源头，在生活中体验数学问题和道理的本质。

【例】解释什么是相遇问题。

①相遇问题的情境导入：一个同学将同桌的作业不小心带回家了，怎么办？

贴近标题的解决方案：打电话约好，两人同时从家出发。

②相遇问题的要素引入：两位同学现场表演，说开始后，同时出发，最后相遇。根据演示过程引导学生说出相遇路程是什么，两人行走的时间有什么关系。

③相遇路程的求法导入：在线段图上标上两人的速度，引导先分步后综合求相遇路程，最后再总结相遇路程的公式。